小明欲將 45 插入如圖所示的二元搜尋樹(Binary Search Tree)，他應該將 45 放到下列那一個節點(node)？（灰色節點為目前有資料的節點）(二元搜尋樹請見選項E)(答案請由A,B,C,D中選一個)
-
A. 丁5.6% (1) -
B. 戊66.7% (12)
-
C. 己5.6% (1)
-
D. 庚11.1% (2)
-
E.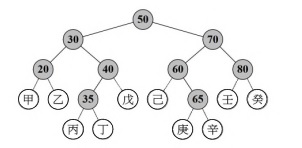
11.1% (2)
解說:
(1)因為45小於樹根50, 所以往樹根的左子樹方向移動
(2)因為45大於節點30, 所以往節點30的右子樹方向移動
(3)因為45大於節點40, 所以往節點40的右子樹方向移動
答案選[戊]
答對率 : 66.7 %
若某完滿二元樹（Full binary tree）有 n 個葉節點（Leaf nodes），則該樹總共有多少個節點？
-
A. n5.6% (1)
-
B. 2n-172.2% (13)
-
C. 2n+116.7% (3)
-
D. log(2n)5.6% (1)
解說:
完滿二元樹（Full binary tree）的每個節點都有兩個子節點，並且所有葉節點都在同一層次上。
如果一棵完滿二元樹有 n 個樹葉節點，則可以使用以下公式來計算總節點數量：
1.在完滿二元樹中，每一層的節點數量是前一層的兩倍，因此若第
k 層有樹葉節點，則該層的節點數量為 2^(k-1)。
k 層有樹葉節點，則該層的節點數量為 2^(k-1)。
2.完滿二元樹的特點是所有內部節點都有兩個子節點，而樹葉節點沒有子節點。因此，樹葉節點的數量
n 與內部節點的數量關係為：
n 與內部節點的數量關係為：
每個內部節點有兩個子節點，因此樹的總節點數量可以由葉節點數量來推算。設內部節點數量為
I，樹葉節點數量為 n，那麼：
I，樹葉節點數量為 n，那麼：
總節點數量=I+n
且每個內部節點貢獻兩個子節點，其中一個是樹葉節點，因此：n=I+1
所以，內部節點數量I會是n−1。
且每個內部節點貢獻兩個子節點，其中一個是樹葉節點，因此：n=I+1
所以，內部節點數量I會是n−1。
3.總節點數量（內部節點加樹葉節點）是：
總節點數量=I+n=(n−1)+n=2n−1
因此，若某完滿二元樹有 n 個葉節點，則該樹總共有 2n−1 個節點。
因此，若某完滿二元樹有 n 個葉節點，則該樹總共有 2n−1 個節點。
答對率 : 72.2 %
高度（height）為 6的完整二元樹（complete binary tree）有幾個節點（node）？
-
A. 645.6% (1)
-
B. 3144.4% (8)
-
C. 250% (0)
-
D. 6350% (9)
解說:
在一棵完整二元樹（complete binary tree）中，每一層的節點數量都是滿的，並且樹的高度（height）定義為根節點到最深葉節點的最長路徑的邊數。
高度為 6 的完整二元樹，我們需要計算樹中節點的總數。
2^(6)-1=63
因此，高度為 6 的完整二元樹有 63 個節點。
2^(6)-1=63
因此，高度為 6 的完整二元樹有 63 個節點。
答對率 : 50 %
「除了樹葉節點外，每一個節點都有兩個子節點的樹」為下列那一種二元樹的定義？
-
A. 完整二元樹（complete binary tree）27.8% (5)
-
B. 完滿二元樹（full binary tree）66.7% (12)
-
C. 完美二元樹（perfect binary tree）5.6% (1)
-
D. 平衡二元樹（balanced binary tree）0% (0)
解說:
下面是對各選項的解釋：
(A) 完整二元樹（complete binary tree）: 一棵完整二元樹是每層節點都被填滿的，除了最後一層外，最後一層的節點則是從左到右填滿的。這種樹不要求每個節點（除了樹葉節點）都擁有兩個子節點。
(B) 完滿二元樹（full binary tree）: 一棵完滿二元樹中的每個節點（除了樹葉節點）都有兩個子節點。這正符合「除了葉節點外，每一個節點都有兩個子節點」的描述。
(C) 完美二元樹（perfect binary tree）: 一棵完美二元樹是指所有節點都完全填滿，並且所有葉節點都在同一層。它的每個節點（除了樹葉節點）也有兩個子節點，因此完美二元樹是完滿二元樹的特例。
(D) 平衡二元樹（balanced binary tree）: 一棵平衡二元樹指的是每個節點的左右子樹高度差不超過一定的數值（如 1）。這種樹的結構不一定要求每個節點（除了樹葉節點）都有兩個子節點。
所以，最符合描述「除了葉節點外，每一個節點都有兩個子節點的樹」的選擇是 (B) 完滿二元樹（full binary tree）。
(A) 完整二元樹（complete binary tree）: 一棵完整二元樹是每層節點都被填滿的，除了最後一層外，最後一層的節點則是從左到右填滿的。這種樹不要求每個節點（除了樹葉節點）都擁有兩個子節點。
(B) 完滿二元樹（full binary tree）: 一棵完滿二元樹中的每個節點（除了樹葉節點）都有兩個子節點。這正符合「除了葉節點外，每一個節點都有兩個子節點」的描述。
(C) 完美二元樹（perfect binary tree）: 一棵完美二元樹是指所有節點都完全填滿，並且所有葉節點都在同一層。它的每個節點（除了樹葉節點）也有兩個子節點，因此完美二元樹是完滿二元樹的特例。
(D) 平衡二元樹（balanced binary tree）: 一棵平衡二元樹指的是每個節點的左右子樹高度差不超過一定的數值（如 1）。這種樹的結構不一定要求每個節點（除了樹葉節點）都有兩個子節點。
所以，最符合描述「除了葉節點外，每一個節點都有兩個子節點的樹」的選擇是 (B) 完滿二元樹（full binary tree）。
答對率 : 66.7 %
在二元搜尋樹進行搜尋時，單次搜尋時間與以下何者成正比？
-
A. 樹的節點總數16.7% (3)
-
B. 樹的高度77.8% (14)
-
C. 樹葉節點的個數5.6% (1)
-
D. 最大鍵值與最小鍵值的差0% (0)
解說:
在二元搜尋樹（Binary Search Tree, BST）進行搜尋時，單次搜尋的時間與樹的高度成正比。這是因為在最壞情況下，你需要沿著樹的高度遍歷節點，才能找到目標節點或確定它不在樹中。
以下是對選項的詳細解釋：
(A) 樹的節點總數: 如果樹是平衡的，搜尋時間與節點總數的對數成正比，因為每次搜索可以排除一半的節點。對於不平衡的樹，節點總數與搜尋時間之間的關係不直接。
(B) 樹的高度: 樹的高度直接影響搜尋的最壞情況時間。對於一棵二元搜尋樹，搜尋的時間複雜度通常是
O(h)，其中 h 是樹的高度。這是因為你可能需要沿著樹的高度進行搜尋。
O(h)，其中 h 是樹的高度。這是因為你可能需要沿著樹的高度進行搜尋。
(C) 樹葉節點的個數: 樹葉節點的數量不直接影響搜尋時間，因為搜尋是基於樹的高度而不是葉節點的數量。
(D) 最大鍵值與最小鍵值的差: 這個差值反映了鍵值的範圍，但不直接影響搜尋時間，因為搜尋時間主要依賴於樹的結構和高度。
因此，單次搜尋時間與樹的高度成正比。
答對率 : 77.8 %